Just click on the images to see them fully. (They were constructed using Fitch, a program that comes with the text Language, Proof & Logic.)
I'm not saying that the proofs are the most elegant or shortest. But they are all complete and correct.
Proof of ¬(P∧Q) → ¬P∨¬Q:

Proof of ¬(P∨Q) → ¬P∧¬Q:

Proof of ¬P∨¬Q → ¬(P∧Q):



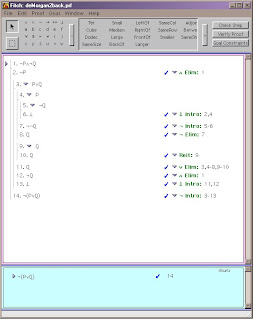
Proof of ¬P∧¬Q → ¬(P∨Q):
Notation:
¬ Negation 'not'
∧ Conjunction 'and'
∨ Disjunction 'or'
→ Conditional 'implies/only if'
⊥ Contradiction
Each vertical line (bar the outermost one) represents a subproof. Each subproof starts with an assumption.
7 comments:
you're awesome!! thank youuu
Could you please explain any one of these more fully? I have just started Intermediate Logic (the Nance book) and am interested in this proof. The book doesn't require it (we use shorter truth tables to show equivalence). I am not sure what the rationale was for some of your steps. Thank you.
Thank you so much!! These are so helpful, just even in understanding how deMorgan's Laws work.
Hello
Can you explain your fourth proof? It's unclear to me what rules you used there.
Better is 4.
1 | ~P^~Q
. -------
2 | ~P ^E:1
3 | ~Q. ^E:1
4 | | PvQ
. | -----
5 | | | P
. | | ---
6 | | | ⊥ ⊥I:2,5
7 | | | Q
. | | ---
8 | | | ⊥ ⊥I:3,7
9 | | ⊥ vE:4,5-6,7-8
10| ~(PvQ) ~I:4-9
Post a Comment